by Medien benutzen vor Wahlen häufig Umfragen, um die jeweiligen Parteienstärken abzuschätzen. Beliebt ist es vor allem, die Umfragen miteinander zu vergleichen, um zu sehen, welche Partei in der Wählergunst gestiegen oder gefallen ist. Wie dieser Beitrag zeigt, werden dabei oftmals statistische Grundsätze übergangen, was zu Interpretationsfehlern führt. Wahlumfragen sind ja regelmäßiger Bestandteil der Nachrichtensendungen wie Heute oder Tagesschau oder in den diversen Tageszeitungen. Die Frage, welche Partei würden sie am kommenden Sonntag wählen, wenn dort eine Bundestagswahl wäre, soll der Öffentlichkeit und den politischen Parteien Informationen über die Stimmung in der Öffentlichkeit geben, wohin die politischen Mehrheiten in Deutschland tendieren. Mich hat schon immer geärgert, wie nachlässig dabei eine statistische Erhebung auf Basis einer Zufallsstichprobe anhand der vorliegenden Prozentzahlen der Stimmenanteile der jeweiligen Parteien in den Medien interpretiert wird. Vorgespiegelte Exaktheit Man behandelt diese Werte, die ja nur Schätzwerte auf Basis einer Zufallsstichprobe darstellen, als quasi exakte Daten, d.h. jeder Wert wird als quasi exakte Abbildung der jeweiligen Stimmenanteile der Grundgesamtheit zum Zeitpunkt der Umfrage interpretiert. Das widerspricht natürlich der eigentlich zugrundeliegenden statistischen Logik.
Topics:
Georg Erber considers the following as important:
This could be interesting, too:
Swiss National Bank writes 2024-11-01 – Data portal – Interest rates and exchange rates, November 2024
investrends.ch writes Fielmann wächst dank US-Zukäufen – Aktie unter Druck
investrends.ch writes Preise für Renditeliegenschaften steigen erneut
investrends.ch writes abrdn Investments lanciert ersten ETF an der SIX
Medien benutzen vor Wahlen häufig Umfragen, um die jeweiligen Parteienstärken abzuschätzen. Beliebt ist es vor allem, die Umfragen miteinander zu vergleichen, um zu sehen, welche Partei in der Wählergunst gestiegen oder gefallen ist. Wie dieser Beitrag zeigt, werden dabei oftmals statistische Grundsätze übergangen, was zu Interpretationsfehlern führt.
Wahlumfragen sind ja regelmäßiger Bestandteil der Nachrichtensendungen wie Heute oder Tagesschau oder in den diversen Tageszeitungen. Die Frage, welche Partei würden sie am kommenden Sonntag wählen, wenn dort eine Bundestagswahl wäre, soll der Öffentlichkeit und den politischen Parteien Informationen über die Stimmung in der Öffentlichkeit geben, wohin die politischen Mehrheiten in Deutschland tendieren. Mich hat schon immer geärgert, wie nachlässig dabei eine statistische Erhebung auf Basis einer Zufallsstichprobe anhand der vorliegenden Prozentzahlen der Stimmenanteile der jeweiligen Parteien in den Medien interpretiert wird.
Vorgespiegelte Exaktheit
Man behandelt diese Werte, die ja nur Schätzwerte auf Basis einer Zufallsstichprobe darstellen, als quasi exakte Daten, d.h. jeder Wert wird als quasi exakte Abbildung der jeweiligen Stimmenanteile der Grundgesamtheit zum Zeitpunkt der Umfrage interpretiert. Das widerspricht natürlich der eigentlich zugrundeliegenden statistischen Logik. Hier sind ja nur Wahrscheinlichkeitsaussagen möglich, d.h. mit einer gewissen Eintrittswahrscheinlichkeit von beispielsweise 95% werden mittels einer Schätzfunktion für den Erwartungswert in der Stichprobe der Umfrage Aussagen über den wahren Wert in der Grundgesamtheit getroffen.
Das mag für den unbedarften Konsumenten nur eine Spitzfindigkeit sein, aber es ist durchaus von erheblicher Relevanz. Zuletzt wurde ja beklagt, dass bei Wahlen oder Plebisziten wie zum Brexit die Prognosen deutlich neben den tatsächlich dann am Wahltag eingetretenen Wahlergebnissen lagen. Man hatte mithin der Öffentlichkeit ein Ergebnis vorhergesagt, dass deutlich von dem tatsächlichen Wahlausgang abwich. Statt einer Mehrheit für den Verbleib Großbritanniens in der EU kam es zu einer Mehrheit für den Brexit. Statt der Wahl von Hillary Clinton zum ersten weiblichen US-Präsidenten wurde Donald Trump in den USA gewählt. Solche Fehlprognosen haben natürlich auch ihre Ursache in der Fehlinterpretation der Genauigkeit der Wahlprognosen durch die Öffentlichkeit.
Anhand eines Beispiels soll dies einmal hier exemplifiziert werden.
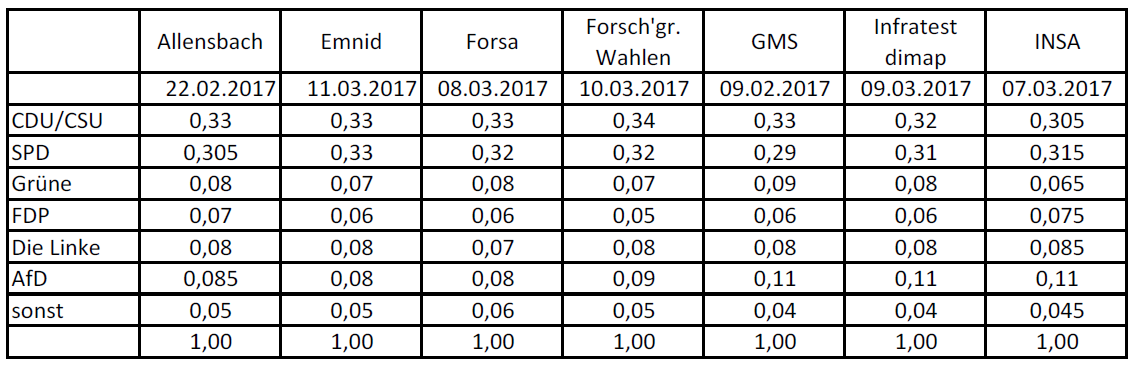
Es geht um aktuelle Umfragen der verschiedenen Umfrageinstitute[ 1 ] zur Sonntagsfrage in Deutschland für die Bundestagswahl 2017 über den Zeitraum vom 9. Februar 2017 bis zum 11. März 2017. In der Regel beträgt die Stichprobengröße rund n = 2500 Befragte. Es gibt marginale Schwankungen von Umfrage zu Umfrage, wie man am Beispiel der Forsa-Umfragen einsehen kann. Diese Schwankungen in der Stichprobengröße sind jedoch weitestgehend unerheblich. Unterschieden werden in den jeweiligen Umfragen sieben Merkmalsausprägungen, d.h. heißt sechs bundesweit agierende Parteien sowie ein Sammelsurium von Splitterparteien, die als sonstige aggregiert ausgewiesen werden.[ 2 ]
Die Umfrageergebnisse waren wie folgt:
Tabelle 1: Umfrageergebnisse bei der Sonntagsfrage zur Bundestagswahl 2017 im Zeitraum Februar und März 2017.[ 3 ]
Mithin hatte die CDU/CSU in der Umfrage von Forsa am 11. März 2017 einen Prozentanteil von 33% der Befragten, usw. usf. Da die Umfrageergebnisse zeitversetzt veröffentlich werden, wird oftmals in den Medien kolportiert, dass die CDU/CSU einen Rückgang von 33% auf 34% zur Umfrage der Forschungsgruppe Wahlen vom 10. März 2017 zu verzeichnen hätte. Macht das Sinn?
Nun bedenken wir, dass die entsprechende Wahrscheinlichkeitsverteilungsfunktion einer solchen Umfrage mit diskreten Merkmalsausprägungen einer Multinomialverteilung entspricht. Diese hat folgende statistische Eigenschaften. Der Erwartungswert E(p(i)) der einzelnen Merkmale entspricht gleich der Anzahl der Befragten n(i), die sich für eine bestimmte Partei i entschieden haben, dividiert durch dir Größe der Stichprobe n, d.h. p(i) = n(i)/n. Es ist die Schätzfunktion des unbekannten Anteilswerts in der Grundgesamtheit, die ja weiterhin unbekannt ist. Mithin ist dies die relative Häufigkeit der Antworten für eine bestimmte Partei. Soweit so gut.
Nun kommt aber der interessantere Teil der schließenden Statistik. Die Varianz, bzw. Streuung der Multinomialverteilung für die einzelnen Anteilswerte ist durch Var(p(i)) = n*p(i)*(1-p(i)) gegeben. Die quadratische Wurzel daraus ergibt die Standardabweichung sigma(p(i)). Diese kann entsprechend mit den relativen Häufigkeiten ebenfalls berechnet werden.
Aus der Statistik wissen wir aber, dass für alle Wahrscheinlichkeitsverteilungen gilt, dass die Erwartungswerte der Verteilungen[ 4 ] , gegen eine Normalverteilung mit wachsender Stichprobengröße konvergieren, d.h. bei großen Stichproben ist es korrekt eine approximative Normalverteilung der Erwartungswerte, d.h. der einzelnen relativen Häufigkeiten der Multinomialverteilung zu unterstellen.[ 5 ]
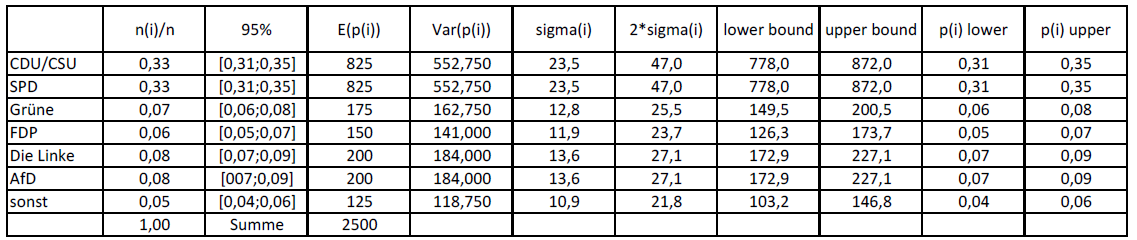
In der Regel wird diese Unsicherheit über die Genauigkeit der Schätzung üblicherweise mittels eines Konfidenzintervalls mit Angabe einer Irrtumswahrscheinlichkeit angegeben. Üblich ist beispielsweise ein 95% Konfidenzintervall, d.h. in den Intervallgrenzen liegt dann mit einer Wahrscheinlichkeit von 95% der wahre Wert in der Grundgesamtheit innerhalb der Intervallgrenzen. Mit 5% Wahrscheinlichkeit liegen sie jedoch außerhalb dieser Grenzen. Dieses Konfidenzintervall ist etwa das Doppelte der Standardabweichung in beide Richtungen, d.h. man berechnet die Ober- und Untergrenze des Konfidenzintervalls in dem man das Doppelte der Standardabweichung vom Mittelwert der jeweiligen relativen Häufigkeit abzieht. In der Tabelle 2 wurden diese Berechnungen Schritt für Schritt am Beispiel der Emnid-Umfrage vom 11. März durchgeführt.
Tabelle 2: Berechnung der Konfidenzintervalle bei der Emnid-Umfrage vom 11. März 2017
In der zweiten Spalte stehen nun die Intervallgrenzen, die wir bei einer Irrtumswahrscheinlichkeit von 5% zugrunde legen müssen, um eine Wahrscheinlichkeitsaussage über den wahren Wert in der Grundgesamtheit der Wähler in der Bundesrepublik Deutschland treffen zu können.
Oftmals Zufallsschwankungen
Statt eines Umfragewerts von 33% für die CDU/CSU wären Werte zwischen 31% und 35% aufgrund der Stichprobenerhebung von 2500 Personen mit der in der Grundgesamtheit mit einer Irrtumswahrscheinlichkeit von 5% konsistent. Erst, wenn diese Grenzen überschritten würden, wäre ein signifikanter Unterschied festzustellen, d.h. es hat sich aus statistischer Sicht wirklich etwas Wesentliches verändert. Alle Änderungen innerhalb des Konfidenzintervalls sind insignifikant, d.h. Zufallsschwankungen in der jeweiligen Zufallsstichprobe. Kehren wir zur Tabelle 1 zurück.
Vergleichen wir die jeweiligen Ergebnisse, dann findet sich nur in der INSA-Umfrage vom 7. März ein signifikanter Unterschied zu allen anderen Umfrageergebnissen für die CDU/CSU. Für die SPD gab es nur bei Allensbach in der Umfrage mit 30,5% und bei GMS mit 29% einen signifikanten Unterschied zur Emnid-Umfrage. Bei den Grünen gab es nur einen signifikanten Unterschied bei der GMS-Umfrage mit 9%. Bei der FDP gab es nur bei INSA eine signifikante Abweichung mit 7,5%. Bei der Partei Die Linke, gab es überhaupt keine signifikanten Abweichungen von den 8%. Bei der Afd sind es nur die Ergebnisse GMS, Infratest dimap und INSA, die signifikant mit 11% abweichen. Es findet daher aus statistischer Sicht eine sehr viel geringere Bewegung der Ergebnisse der Umfragen statt, als es die Interpretation auf Basis der Punktschätzungen mit den relativen Häufigkeiten suggeriert.
Es ist also Anmaßung von Wissen, wenn man jede kleine Abweichung von Werten aus einzelnen Stichprobenerhebungen gleich als signifikante Veränderungen deutet. Vieles ist nur das Ergebnis von Zufallsschwankungen und hat nichts mit einem veränderten Wählerverhalten zu tun.
Es zeigt sich auch bei einer solchen wahrscheinlichkeitstheoretischen Betrachtung, dass es aufgrund der Unschärfe der Stichprobenmethodik nicht möglich ist knappe Ergebnisse aufgrund solcher Erhebungen mit hinreichender Genauigkeit vorherzusagen. Darum ist es keineswegs für den Statistiker überraschend, wenn bei knappen Wahlausgängen die Aussagen, die sich nur auf Punktschätzungen stützen sich als unzutreffend erweisen können. Es ist unter den gegebenen Umständen schlichtweg unmöglich mittels der schließenden Statistik eine verlässliche Vorhersage abzuleiten.
Keine Exaktheit
Wenn man trotzdem in den Medien immer suggeriert es gäbe solche Exaktheit, dann sind das Fake-News. Gerd Gigerenzer hat seit langem versucht hier zu einem aufgeklärteren Bewusstsein beim Umgang mit statischen Analysen beizutragen.[ 6 ] Leider scheint das jedoch häufig ein Kampf gegen Windmühlenflügel zu sein. Eigentlich Schade. Es bräuchte gar nicht so eines großen Aufwandes in den Medien bei der Berichterstattung Intervallschätzungen anstelle von Punktschätzungen einschließlich der damit verbundenen Irrtumswahrscheinlichkeit auszuweisen. Als Daumenregel könnte man sich merken, dass Veränderungen von einem Prozentpunkt nach oben oder nach unten eigentlich nirgendwo eine signifikante statische Veränderung der Anteilswerte signalisieren.
- 1 Allensbach, Emnid, Forsa, Forschungsgruppe Wahlen, GMS, Infratest dimap, INSA.
- 2 CDU/CSU, SPD, Grüne, FDP, Die Linke, AfD und sonstige Parteien.
- 3 Quelle: Wahlrecht
- 4 Sehen wir von Verteilungen ab, wo kein Erwartungswert definiert ist.
- 5 Dieses Ergebnis wird auch zentraler Grenzwertsatz bezeichnet oder auch Gesetz der großen Zahl.
- 6 Gerd Gigerenzer (2002), Über den Umgang mit Zahlen und Risiken. Berlin Verlag, 2002.
©KOF ETH Zürich, 17. Mär. 2017